Destinations
| D1 | D2 | D3 | D4 | ||
| Sources | S1 | 45 | 17 | 21 | 30 |
| S2 | 14 | 18 | 19 | 31 |
Obtain a minimum cost schedule.
Solution:
Since the supply and requirements are not equal it is called an unbalanced transportation problem. In general, if £ai ≠ £bj then it is called an unbalanced transportation problem. We introduce either a dummy row or a column with cost zero quantities and £bi ≠ £aj respectively. Applying Vogel’s approximation method we find the basic feasible solution. Table 2 depicts the basic feasible solution.
Table 2: Basic Feasible Solution using Vogel’s Approximation Method
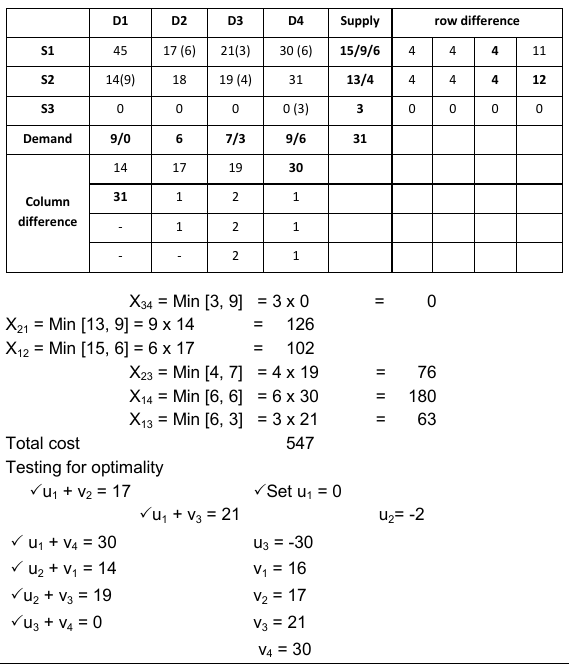

For non-allocated cells, determine cij– uI– vi. Since all the quantities are non-negative, the current solution is optimal. The minimum transportation cost is equal to:
6×17+3×21+6×30+9×14+4×19+3×0 = 547.
This is achieved by transporting x12 = 6 cars from source 1 to destination 2, x13 = 3, x14 = 6 cars from sources 1 to destinations 3 and 4 respectively; x21 = 9 and x33 = 4 cars from sources 2 to destinations 1 and 3 respectively.
Total Views: 40
