Q51242 Use simplex method to solve the LPP

Maximise        Z = 2x1 + 4x2 + x3 + x4

Subject to    x1 + 3x2 + x4 ≤ 4

2x1 + x2 ≤ 3

x2 + 4x3 + x4 ≤ 3

x1, x2, x3, x4 ≥ 0

Rewriting in the standard form

Maximise        Z = 2x1 + 4x2 + x3 + x4 + 0.S1 + 0.S2 + 0.S3

Subject to        x1 + 3x2 + x4 + S1 = 4

2x1 + x2 + S2 = 3

x2 + 4x3 + x4 + S3 = 3

x1, x2, x3, x4, S1, S2, S3 ≥ 0

Solution:

The initial basic solution is x1, x2, x3, x4 = 0, S1 = 4, S2 = 3, S3 = 3

21 8 image 1043

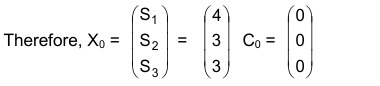
Table 1 depicts the initial table

21 8 image 1044
pivot column * pivot element
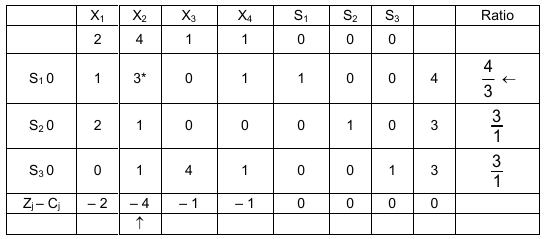
Table No. 1 The Initial Table

S1 is the outgoing variable and x2 is the incoming variable to the basic set. The first iteration gives the table 2:

21 8 image 1045
Table No. 2 The First Iteration Table – X2 is the Incoming Variable

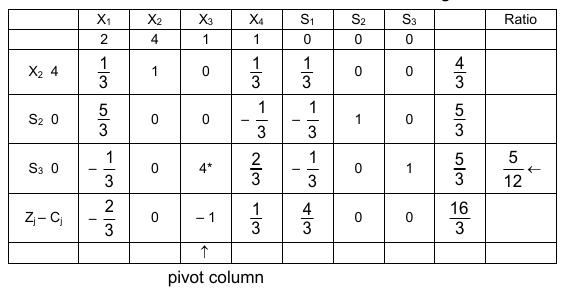
X3 enters the new basic set replacing S3, the second iteration gives the table 3:

21 8 image 1046
Table No. 3 Second Iteration Table – X3 Replaces S3

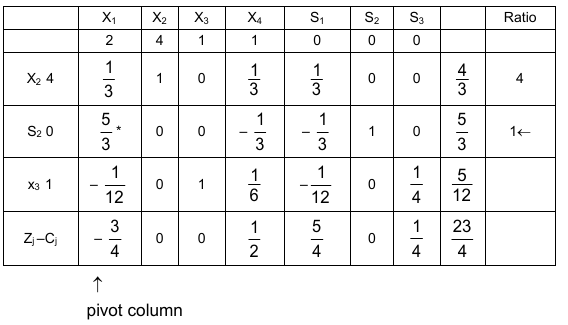
X1 enters the new basic set replacing S2, the third iteration gives the table 4:

21 8 image 1047
Table No. 4 Third Iteration Table – X1 Replaces S2

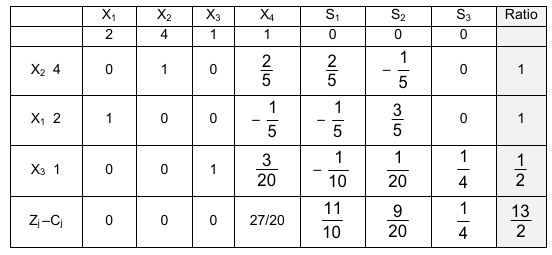
Since all the elements of the last row are non-negative, the optimal solution is Z = 13/2, which is achieved for x2 = 1, x1 = 1,

x3 = 1/2, and x4 = 0.

ed010d383e1f191bdb025d5985cc03fc?s=120&d=mm&r=g

DistPub Team

Distance Publisher (DistPub.com) provide project writing help from year 2007 and provide writing and editing help to hundreds student every year.