Q51241 Maximise z = x1+ 9×2 + x3

Subject to x₁ + 2x₂ + 3x₃  ≤ 9

3x₁ + 2x₂ + 2x₃  ≤ 15

x₁, x2, x3 ≥ 0

Rewriting in the standard form

Maximise z = x₁ + 9x₂ + x₃ + 0.S₁ + 0.S₂

Subject to the conditions

x₁ + 2x₂ + 3x₃ + S₁ = 9

3x₁ + 2x₂ + 2x₃ + S₂ = 15

x₁, x₂, x₃, S₁, S₂ ≥ 0

Where S₁ and S₂ are the slack variables.

Solution:

The initial basic solution is x1, x2, x3 =0, S₁ = 9, S₂ = 15

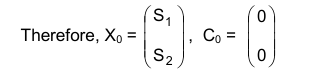
Table 1 depicts the initial simplex table.

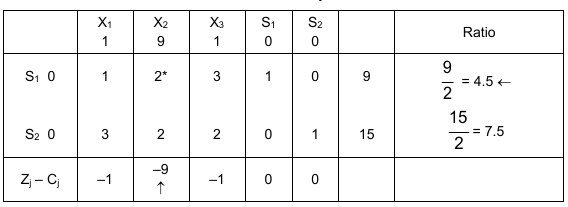
Work column* – pivot element

S₁ – outgoing variable, x₂ – incoming variable

Since the three Z_j – C_j are negative, the solution is not optimal. Choose the maximum negative value that is –9. The corresponding column vector x₂ enters the basis replacing S₁, since ratio is at minimum. You can use the elementary row operations to reduce the pivot element to 1 and other elements of work column to zero.

Divide row 1 with the key element 2 and get the new row. Now make all other elements in the key column zero.

First iteration – The variable x₂ becomes a basic variable replacing S₁ and you obtain the table 2.

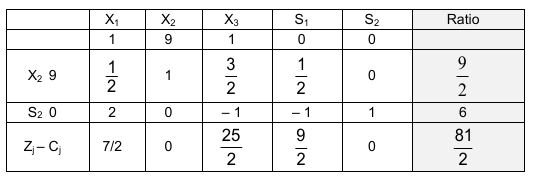
Since all the elements of the last row are non-negative, the optimal solution is obtained. The maximum value of the objective function Z is 81/ 2, achieved for x2= 9/2 S₂ = 6, are the basic variables (refer the shaded column of table 2.). All other variables are non-basic.