| I | II | III | IV | Ui | |
| A | 10 | 12 | 19 | 11 | U1 = 10 |
| B | 5 | 10 | 7 | 8 | U2 = 5 |
| C | 12 | 14 | 13 | 11 | U3 = 8 |
| D | 8 | 15 | 11 | 9 | U4 = 2 |
| Vj | V1 = 5 | V2 = 8 | V3 = 7 | V4 = 9 |
Total Ui = SUi = 25
Total Vj = SVj = 29
Solution
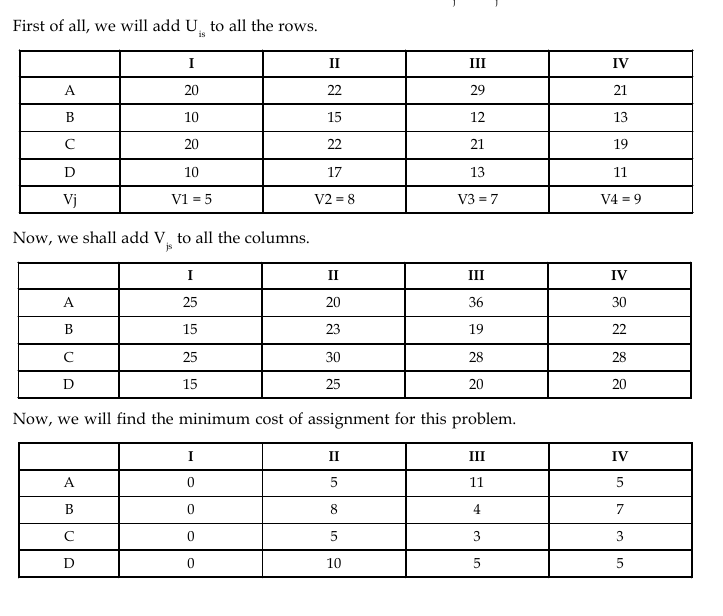
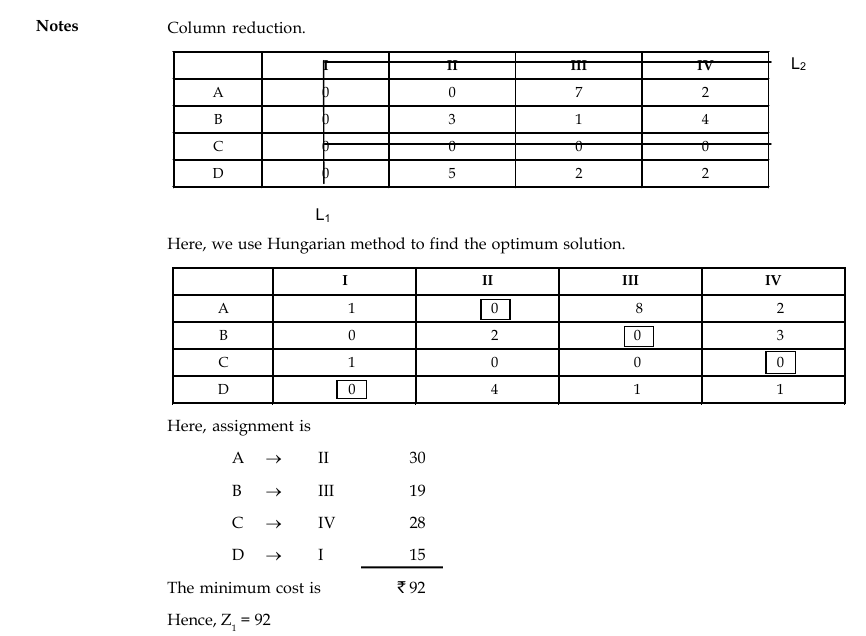
We got the cost matrix for Z1 by adding U1 to different rows and Vj to different columns of cost matrix for Z.
Hence, Z1 = Z + SUi + SVj
i.e., 92 = 38 + 25 + 29
Observe that the assignment for both the matrix is same. Hence, we can say that Z is minimized whenever Z1 is minimized. However, the solution (minimised cost for Z = and Z1) will be different due to cost elements (Cij).
Total Views: 13
