Q51187 A manufacturing company has four plants situated at different locations, all producing the same product. The manufacturing cost varies at each plant due to internal and external factors. The size of each plant varies, and hence the production capacities also vary. The cost and capacities at different locations are given in the following table:

Particulars			Plant
	A	B	C	D
Production cost per unit (Rs.)	18	17	15	12
Capacity	150	250	100	70

The company has five warehouses. The demands at these warehouses and the transportation costs per unit are given in the Table 2 below. The selling price per unit is ₹ 30.

Warehouse		Transportation cost (Rs) — Unit-wise			Demand
	A	B	C	D
1	6	9	5	3	100
2	8	10	7	7	200
3	2	6	3	8	120
4	11	6	2	9	80
5	3	4	8	10	70

1. Formulate the problem to maximize profits.
2. Find the total profit.

Solution:

1. The objective is to maximize the profits. Formulation of transportation problem as profit matrix table is shown in Table 3. The profit values are arrived as follows.

Profit = Selling Price –Production cost –Transportation cost

		Destination
	A	B	C	D	Demand
1	6	4	10	15	100
2	4	3	8	11	200
3	10	7	12	10	120
4	1	7	13	9	80
5	9	9	7	8	70
Supply	150	250	100	70	570

Converting the profit matrix to an equivalent loss matrix by subtracting all the profit values in Table No. 3 from the highest value 13. Subtracting all the values from 13, the loss matrix obtained is shown in the Table 4.

Destination

	A	B	C	D	Demand
1	9	11	5	0	100
2	11	12	7	4	200
3	5	8	3	5	120
4	14	8	2	6	80
5	6	6	8	7	70
Supply	150	250	100	70	570

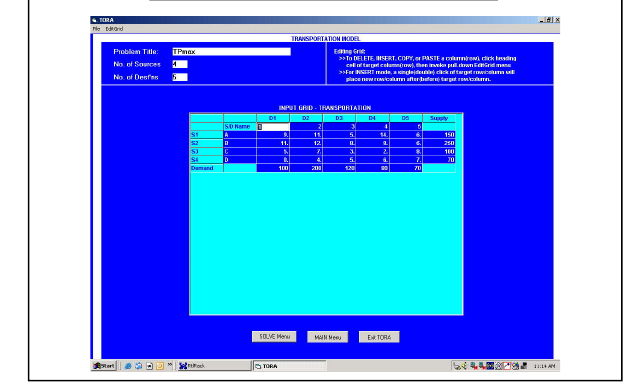
2. To determine the initial solution using TORA

Input Screen:

Output Screen:

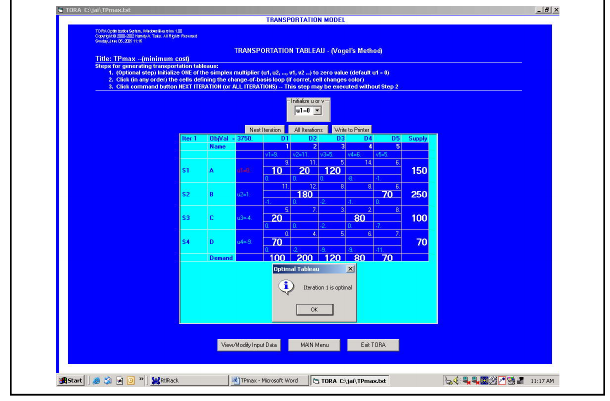
The first iteration itself is optimal, hence optimality is reached.

3. To find the total cost:

The total maximization profit associated with the solution is

Total Profit       = (6 × 10) + (4 × 20) + (10 × 120) + (3 × 180) + (9 × 70) + (10 × 20) + (13 × 80) + (15 × 70)

= 60 + 80 + 1200 + 540 + 630 + 200 + 1040 + 1050

= ` 4800.00