MS-008: Quantitative Analysis For Managerial Applications last 3 yrs paper
June, 2021
- Solve the following system of linear equations, using matrix method or any other method that you prefer:
2x + 3y + 3z = 5
x – 2y + z = – 4
3x – y – 2z = 3
- What do you understand by the terms Primary data and Secondary data? Explain some of the points to be kept in mind while designing a questionnaire.
- What do you mean by Probability? What are the different approaches to Probability theory? Explain it with the help of an example.
- A marketing research firm wants to estimate the share that foreign companies have in the Indian market for certain products. A random sample of 100 consumers is obtained, and it is found that 34 people in the sample are the users of foreign-made products; the rest are users of domestic products. Give a 95% confidence interval for the share of foreign products in this market. (The value of test statistic at 95% confidence level is 126)
- What do you mean by Time Series Analysis? How would you conduct such an analysis for forecasting the sales of a product in your firm?
- Write short notes on any three of the following
(a) Conditions of Maxima and Minima
(b) Mathematical Properties of Median
(c) Exponential Distribution
(d) Stratified Sampling
(e) Least Square Criterion.
- An aircraft manufacturer is concerned about variability in the diameters of lids used to seal fuel tanks. Only a narrow range of diameters is acceptable. A sample of 20 fuel-tank lids is taken. After measuring the 20 diameters, an engineer finds them to have a standard deviation of 0.095 inches. Conduct a test at 2% level of significance to see whether population variation of lid diameters equals 0.0001 inches squared, as specified by engineers.
(The value of test statistic at = 0.01, 19 degrees of freedom is 36.91)
(The value of test statistic at = 0.99 is 7.633 at 19 degrees of freedom - Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all the students who reside in hostel attain A-grade in their annual examination and 20% of day scholars attain A-grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A-grade. What is the probability that the student is a hosteler
SECTION A
SECTION B
December, 2020
- Suppose the price p and quantity q of a commodity are related by the equation:
q = 30 – 4p – p
find:
(i) Elasticity of demand, eq defined as = -dp/q /dp/p at p = 2, andMarginal Revenue (MR) defined as = dR/ dq , where R = p.q.
- Explain arithmetic mean along with its properties. Also explain the relationship among mean, mode and median with the help of a diagram
- What do you understand by decision theory? What are the various key issues in decision theory? Explain decision tree approach also.
- A stock-market analyst wants to estimate the average return on a certain stock. A random sample of 15 days yields an average (annualized) rent of 10.37% and sample standard deviation is 3.5. Assuming a normal distribution of returns, give a 95% confidence interval for the average return on this stock. (The value for given statistic at n = 14 is 2.145).
- What are long-term decisions? What are the various methods used in forecasting long-term decisions?
- Write short notes on any three of the following
(a) Classification of statistical methods
(b) Guidelines for choosing the classes
(c) Random variable
(d) Type I and Type II error
(e) Correlation coefficient
- A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the 2 bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that it is drawn from 1st bag.
- In a group of 300 students, each person is asked about his/her favourite subject area. Based on data given below, is it reasonable to conclude that subject preference is independent of the gender
SECTION A
SECTION B
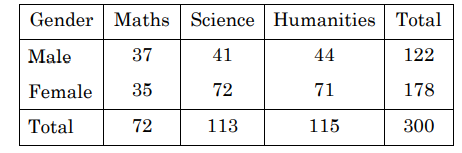
Taking the significance level as 5%.
(The value of test statistic at 2 degree of freedom is 5.991)
June, 2020
- Define matrices. Give examples of some special matrices. How would you represent the data of a transportation problem and a pity-off matrix in the matrix form?
- Consider the following data which relate to the sales of 100 conipanies:
- Bag A contains 2 white and 3 red balls and bag B contains 4 white and 5 red balls. One ball is drawn at random and is found to be red. Find the probability that it was drawn from bag A.
- What is a Chi-square distribution? How would you use it in testing the goodness of fit and testing independence of categorised data?
- A supplier of components to an electronic industry makes a product which sometimes fail immediately it is used. He controls his manufacturing process so that the proportion of faulty products is supposed to be only 5%. Out of•400 units in one batch 26 proved to be faulty. Verify the manufacture’s claim. Use 0.05 level of significance. Given value of test statistic at this level of significance is 1.96.
- Write short notes on any three of the following
(a) Null Matrix
(b) Shewness
(c) Poisson distribution
(d) Systematic sampling
(e) Rank Correlation
- Calculate correlation coefficient from the following data:
- Describe the concept and significance of measures of central tendency. Define quantiles and discuss how would you compute several quantiles such as quartiles, deciles and percentiles.
SECTION A
| Sales(in lakhs) | No. of Compaines |
| 40-50 | 5 |
| 50-60 | 15 |
| 60-70 | 255 |
| 70-80 | 30 |
| 80-90 | 20 |
| 90-100 | 5 |
SECTION B
| X | Y |
| 100 | 30 |
| 200 | 50 |
| 300 | 60 |
| 400 | 30 |
| 500 | 100 |
| 600 | 110 |
| 700 | 130 |
Also view
- IGNOU Course details and sample paper link
- Sample paper of ignou for exam
- Solved Assignments of IGNOU courses
Total Views: 51
