Q51281 The maintenance manager of a chemical company is interested in determining a rational policy for maintenance of pneumatic conveying equipment. The equipment is a part of the process line and affects production. It has one bearing each on the inlet side (A) and the outlet side (B). Whenever there is a failure of any bearing, it has to be replaced immediately. The company has a good system of maintaining records on performance of the equipment and the failure records are available.

Given the cost of the bearings, the cost of downtime of equipment and the time taken to replace either one bearing or both the bearings, you can use a simulation model to find out the best alternative solution for a given set of constraints. For the above scenario, the following failure data is available:

Table 1 depicts the equipment performance data

	No. of failures
Age at failure	Inlet side	Outlet side
(hours)	Bearing (A)	Bearing (B)
150	7	0
300	16	3
450	18	9
600	23	12
750	14	16
900	10	18
1,050	7	33
1,200	5	7
1,350	0	2

The cost of bearing is Rs. 300 each for ‘A’ and Rs. 500 each for ‘B’. The cost of downtime of equipment is Rs. 700 per hour and it takes 2 hours to replace one bearing either at inlet or outlet side and 3 hours to replace both the bearings. The three maintenance policies to be evaluated are:

1. Replace a bearing only when it fails.
2. Replace both the bearings if one fails.
3. Replace the bearing which fails plus the other one if it has been in use for more than its estimated average services life – 600 hours for bearing A and 860 hours for bearing B

Find the best alternative through simulation.

Solution:

It is assumed that the failure of a bearing is independent of the maintenance policy followed. Random numbers are allocated for different failure times: (Table 2 depicts the random numbers)

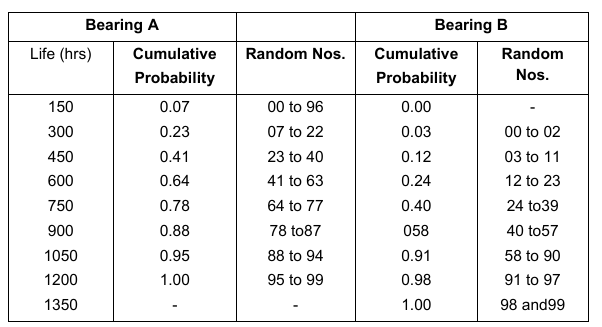
We can now select random numbers from the tables and generate a set of 12 bearings for each of the bearings. Table 3 depicts the set of 12 bearing for each of the bearings generated.

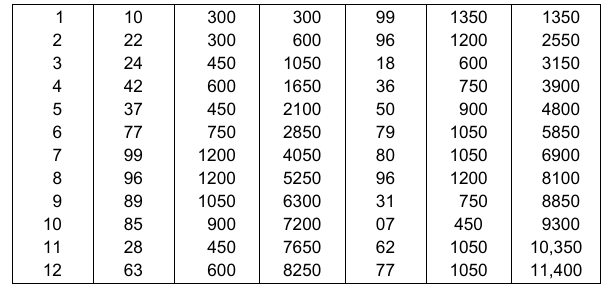
Let us compare the costs of three policies for the first 7200 hours.

Policy 1: Replace a bearing only when it fails.

‘A’ requires replacement 10 times, and ‘B’ 7 times during this period as seen from the lives of successive bearings.

Total cost = (300 × 10 + 500 × 7) + (17 × 2 × 700) = Rs. 30, 300

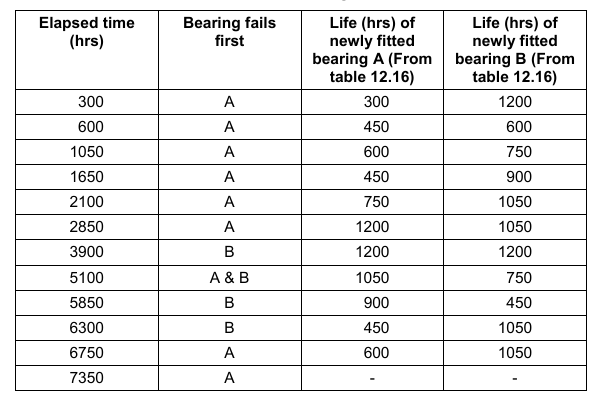
Policy 2: Replace both the bearing if one fails. Table 4 depicts bearing failure information.

Policy 3 is the cheapest.

The simulation is limited to 7200 hours of operation since the purpose is only to illustrate the method. With such small number of trials the results may turn out to be erratic. Consider policy 1 again. With a different set of random numbers and extended simulation, there may be occasions of both bearing failing at the same time, thus affecting the cost of downtime for replacement. Simulation with sufficiently large number of trials can only lead to dependable decisions.

Table 5 depicts the bearing record.

This will be the life (from Table 5) if newly fitted. For survivors from previous replacement, this will be the balance life (col. 8)

.