Answer:
Sensitivity analysis involves ‘what if?’ questions. In the real world, the situation is constantly changing like change in raw material prices, decrease in machinery availability, increase in profit on one product, and so on. It is important to decision makers for find out how these changes affect the optimal solution. Sensitivity analysis can be used to provide information and to determine solution with these changes.
Sensitivity analysis deals with making individual changes in the coefficient of the objective function and the right hand sides of the constraints. It is the study of how changes in the coefficient of a linear programming problem affect the optimal solution.
Change in the Right-hand Side Constraints Values and Effect on Optimal Solution
Suppose an additional 40 kgs of material 3 is available, the right-hand side constraint increases from 150 to 190 kgs.
Now, if the problem is solved, we get the optimal values as x1 = 23.61, x2 = 16.11 and Zmax = 1427.78
From this, we can infer that an additional resources of 40 kgs increases the profit by = 1427.78 –
1250 = ₹ 177.78
Therefore, for one kg or one unit increase, the profit will increase by
= 177.78/40
= ₹ 4.44
Dual price is the improvement in the value of the optimal solution per unit increase in the right- hand side of a constraint. Hence, the dual price of material 3 is ₹ 4.44 per kg.
Increase in material 2 will simply increase the unused material 2 rather than increase in objective function. We cannot increase the RHS constraint values or the resources. If the limit increases, there will be a change in the optimal values.
The limit values are given in Table 2.10, i.e., Min RHS and Max RHS values.
For example, for material 3, the dual price ₹ 4.44 applies only to the limit range 150 kgs to 262.50 kgs.
Where there are simultaneous changes in more than one constraint RHS values, the 100 Per cent Rule must be applied.
Reduced Cost
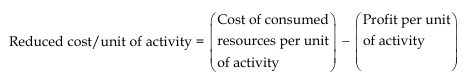
If the activity’s reduced cost per unit is positive, then its unit cost of consumed resources is higher than its unit profit, and the activity should be discarded. This means that the value of its associated variable in the optimum solution should be zero.
Alternatively, an activity that is economically attractive will have a zero reduced cost in the optimum solution signifying equilibrium between the output (unit profit) and the input (unit cost of consumed resources).
In the problem, both x1 and x2 assume positive values in the optimum solution and hence have zero reduced cost.
Considering one more variable x3 with profit ₹ 50 Zmax = 40×1 + 30×2 + 50×3
Subject to constraints,
4x1 + 5x2 + 6x3≤175 (a)
2x2 + 1x3≤ 50 (b)
6×1 + 3×2 + 3×3≤ 150 (c)
where x1, x2, x3 ³ ≤ 0
The sensitivity analysis of the problem is shown in the computer output below in Figure1
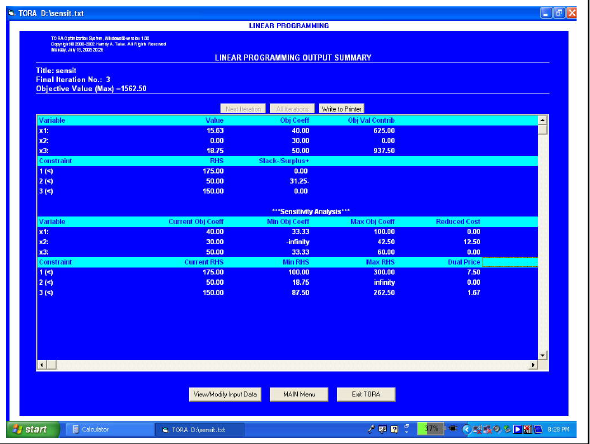
The reduced cost indicates how much the objective function coefficient for a particular variable would have to improve before that decision function assumes a positive value in the optimal solution.
The reduced cost of ₹12.50 for decision variable x2 tells us that the profit contribution would have to increase to at least 30 + 12.50 = 42.50 before x 3 could assume a positive value in the optimal solution.
Total Views: 4
