Multiple choice question for engineering
Set 1
1. A CFG is ambiguous if
a) It has more than one rightmost derivations
b) It has more than one leftmost derivations
c) No parse tree can be generated for the CFG
d) None of the mentioned
Answer
Answer: b [Reason:] A context free grammar is ambiguous if it has more than one parse tree generated or more than one leftmost derivations. An unambiguous grammar is a context free grammar for which every valid string has a unique leftmost derivation.
2. Which of the following are always unambiguous?
a) Deterministic Context free grammars
b) Non-Deterministic Regular grammars
c) Context sensitive grammar
d) None of the mentioned
Answer
Answer: a [Reason:] Deterministic CFGs are always unambiguous , and are an important subclass of unambiguous CFGs; there are non-deterministic unambiguous CFGs, however.
3. A CFG is not closed under
a) Dot operation
b) Union Operation
c) Concatenation
d) Iteration
Answer
Answer: d [Reason:] The closure property of a context free grammar does not include iteration or kleene or star operation.
4. Which of the following is an real-world programming language ambiguity?
a) dangling else problem
b) halting problem
c) maze problem
d) none of the mentioned
Answer
Answer: a [Reason:] Dangling else problem: In many languages,the else in an if-then-else statement is optional, which results into nested conditionals being ambiguous, at least in terms of the CFG.
5. Which of the following is a parser for an ambiguous grammar?
a) GLR parser
b) Chart parser
c) All of the mentioned
d) None of the mentioned
Answer
Answer: c [Reason:] GLR parser: a type of parser for non deterministic and ambiguous grammar
Chart parser: aa type of parser for ambiguous grammar.
6. A language that admits only ambiguous grammar:
a) Inherent Ambiguous language
b) Inherent Unambiguous language
c) Context free language
d) Context Sensitive language
Answer
Answer: a [Reason:] A context free language for which no unambiguous grammar exists, is called Inherent ambiguous language.
7. Which of the following is an example of inherent ambiguous language?
a) {an|n>1}
b) {anbncmdm| n,m > 0}
c) {0n1n|n>0}
d) None of the mentioned
Answer
Answer: b [Reason:] This set is context-free, since the union of two context-free languages is always context free.
8. State true or false:
Statement: R->R|T T->ε is an ambiguous grammar
a) true
b) false
Answer
Answer: a [Reason:] The production can be either itself or an empty string. Thus the empty string has more than one leftmost derivations, depending on how many times R->R is being used.
9. In context to ambiguity, the number of times the following programming statement can be interpreted as:
Statement: if R then if T then P else V
a) 2
b) 3
c) 4
d) 1
Answer
Answer: a [Reason:] Dangling else problem
if R then (if T then P else V) and if R then (if T then P) else V are the two ways in which the given if else statement can be parsed.
10. CFGs can be parsed in polynomial time using__________
a) LR parser
b) CYK algorithm
c) SLR parser
d) None of the mentioned
Answer
Answer: CYK algorithm parses the CFG in polynomial time while LR parsers do the same in linear time. DCFGs are accepted by DPDAs and parsed using LR parsers or CYK algorithm.
Set 2
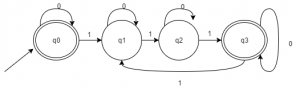
1. Given Language: {x | it is divisible by 3}
The total number of final states to be assumed in order to pass the number constituting {0, 1} is
a) 0
b) 1
c) 2
d) 3
Answer
Answer: c [Reason:] The DFA for the given language can be constructed as follows:
2. A binary string is divisible by 4 if and only if it ends with:
a) 100
b) 1000
c) 1100
d) 0011
Answer
Answer: a [Reason:] If the string is divisible by four, it surely ends with the substring ‘100’ while a binary string divisible by 2 would surely end with the substring ‘10’.
3. Let L be a language whose FA consist of 5 acceptance states and 11 non final states. It further consists of a dumping state. Predict the number of acceptance states in Lc.
a) 16
b) 11
c) 5
d) 6
Answer
Answer: a [Reason:] If L leads to FA1, then for Lc, the FA can be obtained by exchanging the final and non-final states.
4. If L1 and L2 are regular languages, which among the following is an exception?
a) L1 U L2
b) L1 – L2
c) L1 ∩ L2
d) All of the mentioned
Answer
Answer: d [Reason:] It the closure property of Regular language which lays down the following statement:
If L1, L2 are 2- regular languages, then L1 U L2, L1 ∩ L2, L1C, L1 – L2 are regular language.
5. Predict the analogous operation for the given language:
A: {[p, q] | p ϵ A1, q does not belong to A2}
a) A1-A2
b) A2-A1
c) A1.A2
d) A1+A2
Answer
Answer: a [Reason:] When set operation ‘-‘ is performed between two sets, it points to those values of prior set which belongs to it but not to the latter set analogous to basic subtraction operation.
6. Which among the following NFA’s is correct corresponding to the given Language?
L= {xϵ {0, 1} | 3rd bit from right is 0}
a) 
b) 
c) 
d) None of the mentioned
Answer
Answer: a [Reason:] The NFA accepts all binary strings such that the third bit from right end is 1 and if not, is send to Dumping state. Note: It is assumed that the input is given from the right end bit by bit.
7. Statement 1: NFA computes the string along parallel paths.
Statement 2: An input can be accepted at more than one place in an NFA.
Which among the following options are most appropriate?
a) Statement 1 is true while 2 is not
b) Statement 1 is false while is not
c) Statement 1 and 2, both are true
d) Statement 1 and 2, both are false
Answer
Answer: c [Reason:] While the machine runs on some input string, if it has the choice to split, it goes in all possible way and each one is different copy of the machine. The machine takes subsequent choice to split further giving rise to more copies of the machine getting each copy run parallel. If any one copy of the machine accepts the strings, then NFA accepts, otherwise it rejects.
8. Which of the following options is correct for the given statement?
Statement: If K is the number of states in NFA, the DFA simulating the same language would have states less than 2k.
a) True
b) False
Answer
Answer: a [Reason:] If K is the number of states in NFA, the DFA simulating the same language would have states equal to or less than 2k.
9. Let N (Q, ∑, δ, q0, A) be the NFA recognizing a language L. Then for a DFA (Q’, ∑, δ’, q0’, A’), which among the following is true?
a) Q’ = P(Q)
b) Δ’ = δ’ (R, a) = {q ϵ Q | q ϵ δ (r, a), for some r ϵ R}
c) Q’={q0}
d) All of the mentioned
Answer
Answer: d [Reason:] All the optioned mentioned are the instruction formats of how to convert a NFA to a DFA.
10. There exists an initial state, 17 transition states, 7 final states and one dumping state, Predict the maximum number of states in its equivalent DFA?
a) 226
b) 224
c) 225
d) 223
Answer
Answer: a [Reason:] The maximum number of states an equivalent DFA can comprise for its respective NFA with k states will be 2k.
Set 3
1. To derive a string using the production rules of a given grammar, we use:
a) Scanning
b) Parsing
c) Derivation
d) All of the mentioned
Answer
Answer: b [Reason:] Parsing is required to check the acceptability of a string. Further, comes the syntactical phase which is taken care by other phases of compiler.
2. Which of the following parser reaches the root symbol of the tree at last?
a) Top down parser
b) Bottom up parser
c) TOP down and Bottom up parser
d) None of the mentioned
Answer
Answer: b [Reason:] Bottom up parser starts from the bottom with the string and comes up to the start symbolusing a parse tree or a derivation tree.
3. Left corner parsing methof uses which of the following?
a) Top down parser
b) Bottom up parser
c) TOP down and Bottom up parser
d) None of the mentioned
Answer
Answer: c [Reason:] It is a hybrid method which works bottom up along the left edges of each subtree, and top down on the rest of the parse tree.
4. Which of the following parser performs top down parsing?
a) LALR parser
b) LL parser
c) Recursive Accent parser
d) None of the mentioned
Answer
Answer: b [Reason:] Bottom up parsing is done by shift reduce parsers like LALR parsers, Operator precedence parsers, simple precedence parsers, etc.
5. Which of the following is true for shift reduce parsers?
a) Scans and parses the input in one forward pass over the text, without any backup.
b) A shift command advances in the input stream by one symbol
c) LALR parser
d) All of the mentioned
Answer
Answer: d [Reason:] The mentioned are the correct and proper functions of a shift reduce parsers. The parsing methods are most commonly used for parsing programming languages, etc.
6. State true or false:
Statement: LALR parsers uses tables rather than mutually recursive functions.
a) true
b) false
Answer
Answer: b [Reason:] It is exactly the opposite case where LALR parsers uses mutually recursive functions instead of tables. It is a simplified version of canonical left to right parser.
7. LALR in LALR parser stands for:
a) Left aligned left right parser
b) Look ahead left to right parser
c) Language Argument left to right parser
d) None of the mentioned
Answer
Answer: [Reason:] LALR stands for Look ahead left to right parsers. It has more language recognition power than LR(0) parser.
8. Which of the following can be a LALR parser generator?
a) YACC
b) GNU Bison
c) YACC and GNU Bison
d) None of the mentioned
Answer
Answer: c [Reason:] YACC is a computer code for UNIX operating system which generates a LALR parser. On the other hand GNU Bison or Bison can generate LALR and GLR parsers.
9. Which of the following parsers do not relate to Bottom up parsing?
a) LL parser
b) Recursive descent parser
c) Earley parsers
d) All of the mentioned
Answer
Answer: d [Reason:] All the following mentioned are top down parsers and begin their operation from the starting symbol.
10. Which of the following is true for a predictive parser?
a) Recursive Descent parser
b) no backtracking
c) Recursive Descent parser and no backtracking
d) None of the mentioned
Answer
Answer: c [Reason:] Predictive parsing is possible only for the class of LL-grammars, which are the CFG for which there exists some positive integer k that allows a recursive descent parser to decide which production to use by examining only the next k tokens of input.
Set 4
1. Which kind of proof is used to prove the regularity of a language?
a) Proof by contradiction
b) Direct proof
c) Proof by induction
d) None of the mentioned
Answer
Answer: a [Reason:] We use the method of proof by contradiction in pumping lemma to prove that a language is regular or not.
2. The language of balanced paranthesis is
a) regular
b) non regular
c) may be regular
d) none of the mentioned
Answer
Answer: b [Reason:] Given n, there is a string of balanced parentheses that begins with more than p left parentheses, so that y will contain entirely of left parentheses. By repeating y, we can produce a string that does not contain the same number of left and right parentheses, and so they cannot be balanced.
3. State true or false:
Statement: Pumping lemma gives a necessary but not sufficient condition for a language to be regular.
a) true
b) false
Answer
Answer: a [Reason:] The converse of the lemma is not true. There may exists some language which satisfy all the conditions of the lemma and still be non-regular.
4. Which of the following is/are an example of pigeon hole principle?
a) Softball team
b) Sock picking
c) Hair counting
d) All of the mentioned
Answer
Answer: d [Reason:] There are several applications of pigeonhole principle:
Example: The softball team: Suppose 7 people who want to play softball(n=7 items), with a limitation of only 4 softball teams to choose from. The pigeonhole principle tells us that they cannot all play for different teams; there must be atleast one team featuring atleast two of the seven players.
5. Pigeonhole principle can be applied in the following computer science algorithms:
a) hashing algorithm
b) lossless compression algorithm
c) both (a) and (b)
d) none of the mentioned
Answer
Answer: c [Reason:] Collisions are inevitable in a hash table because the number of possible keys exceeds the number of indices in the array.
6. If n objects are distributed over m places, and n < m, then some of the places receive:
a) at least 2 objects
b) at most 2 objects
c) no object
d) none of the mentioned
Answer
Answer: c [Reason:] This is one of the alternative formulations of the pigeon hole principle. As n < m, there will exist some place which will not receive any of the object.
7. Which of the following fields may have pigeonhole principle violated?
a) Discrete mathematics
b) Computer Science
c) Quantum Mechanics
d) None of the mentioned
Answer
Answer: c [Reason:] Y Aharonov proved mathematically the violation of pigeon hole principle in Quantum mechanics and proposed inferometric experiments to test it.
8. Which of the following is not an application of Pumping Lemma?
a) {0i1i|i>=0}
b) {0ix|i>=0, x∈{0, 1}* and |x|<=i}
c) {0n| n is prime}
d) None of the mentioned
Answer
Answer: d [Reason:] None of the mentioned are regular language and are an application to the technique Pumping Lemma. Each one of the mentioned can be proved non regular using the steps in Pumping lemma.
9. Which of the following can refer a language to be non regular?
a) Pumping Lemma
b) Myphill Nerode
c) Both (a) and (b)
d) None of the mentioned
Answer
Answer: c [Reason:] On the contrary, the typical way to prove that a language is to construct either a finite state machine or a regular expression for the language.
10. Which of the following is not an example of counting argument?
a) Pigeonhole principle
b) Dirichlet’s drawer principle
c) Dirichlet’s box principle
d) None of the mentioned
Answer
Answer: d [Reason:] Pigeon hole principle or Dirichlet’s drawer principle or Dirichlet’s box principle is an example of counting argument whose field is called Combinatorics.
Set 5
1. Which of the given problems are NP-complete?
a) Node cover problems
b) Directed Hamilton Circuit Problem
c) Both (a) and (b)
d) None of the mentioned
Answer
Answer: c [Reason:] Vertex cover or Node cover problem, and Hamilton Circuit problem, both are NP complete type of problems.
2. Which of the following problems do not belong to Karp’s 21 NP-complete problems?
a) Vertex Cover problems
b) Knapsack
c) 0-1 integer programming
d) None of the mentioned
Answer
Answer: d [Reason:] There exists a set of 21 problems that are NP-complete and the set is called Karp’s 21 NP-complete problems.
3. Which of the following problems were reduced to Knapsack?
a) Exact Cover
b) Max Cut
c) 0-1 integer programming
d) None of the mentioned
Answer
Answer: a [Reason:] Exact cover is a decision problem in computer science to determine if an exact cover exists.
4. An exact cover problem can be represented using:
a) incidence matrix
b) bipartite graph
c) both (a) and (b)
d) none of the mentioned
Answer
Answer: c [Reason:] The relation ‘contains’ can be represented using a bipartite graph. The vertices of the graph can be divided into two disjoint sets, one representing the subset S and the other representing the elements of P and one edge for each subset in S;each node is included in exactly one of the edges forming the cover.
5. For which of the following, greedy algorithm finds a minimal vertex cover in polynomial time?
a) tree graphs
b) bipartite graphs
c) both (a) and (b)
d) none of the mentioned
Answer
Answer: a [Reason:] For bipartite graphs, Konigs theorem allows the bipartite vertex problem to be solved in polynomial time.
6. Hamilton circuit problem can have the following version/s as per the input graph:
a) directed
b) undirected
c) both (a) and (b)
d) none of the mentioned
Answer
Answer: c [Reason:] Hamilton circuit problem is a problem determining whether a Hamiltonian path(a path in an undirected or directed graph that visits each vertex exactly once) exists in a graph(directed or undirected).
7. Hamilton Circuit problem is a special case of ____________
a) travelling salesman problem
b) halting problem
c) hitting set
d) none of the mentioned
Answer
Answer: a [Reason:] Hamilton circuit problem is a special case of travelling salesman problem, obtained by setting the distance between two cities to one if they are adjacent and two otherwise, and verifying that the total distance travelled is equal to n (if so, the route is a Hamiltonian circuit; if there is no Hamiltonian circuit then the shortest route will be longer).
8. Which of the following cannot solve Hamilton Circuit problem?
a) DNA Computer
b) Monte Carlo algorithm
c) Dynamic programming
d) None of the mentioned
Answer
Answer: d [Reason:] Using Inclusion-exclusion principle, Andreas showed how to solve Hamilton Circuit problem in arbitrary n-vertex graphs by a Monte Carlo algorithm in time O(1.657n).
9. State true or false:
Statement: Hamiltonian cycles through any fixed edge is always even, so if one such cycle is given, the second one must also exists.
a) true
b) false
Answer
Answer: a [Reason:] Handshaking lemma states that ‘Every finite undirected graph has an even number of vertices with odd degree.
10. Fibonacci number falls in the category of _________ combinatorics.
a) Algebric
b) Enumerative
c) Analytic
d) Extremal
Answer
Answer: b [Reason:] Enumerative combinatorics is the most classical area of combinatorics and concentrates on counting the number of certain combinatorial objects. Fibonacci series is a basic example of Enumerative Combinatorics.
Total Views: 11
