MS-051: Operations Research last 3 yrs paper
June, 2021
- “An operations research team consists of trained researchers utilizing the skills and tools of applicable sciences.” Explain some tools and techniques used by operations research team.
- What is integer linear programming? Explain the merits and demerits of “rounding off the continuous optimum of a linear programming problem.”
- A local travel agent is planning a charter trip to a major sea port. The eight day/seven night package includes the fare for round trip, surface transportation, board and lodging and selected tour options. The charter trip is restricted to 200 persons and the past experience indicates that there will not be any problem for getting 200 clients. The problem for the travel agent is to determine the number of Deluxe, Standard and Economy tour packages to offer for this charter. These three plans differ according to seating and service for the flight, quality of accommodations, meal plans and tour options. The following table summarizes the estimated prices for the three packages and the corresponding expenses for the travel agent. The travel agent has hired an aircraft for the flat fee of ` 2,00,000 for the entire trip. In planning the trip, the following considerations must be taken into account:
(i) At least 10% of the packages must be Deluxe type.
(ii) At least 35% but not more than 70% must be the Standard type.
(iii) At least 30% must be of the Economy type.
(iv) The maximum number of Deluxe packages available in any aircraft is restricted to 60.
(v) The hotel desires that at least 120 of the tourists should be on the Deluxe and Standard packages taken together.
Price and costs for tour packages per person:
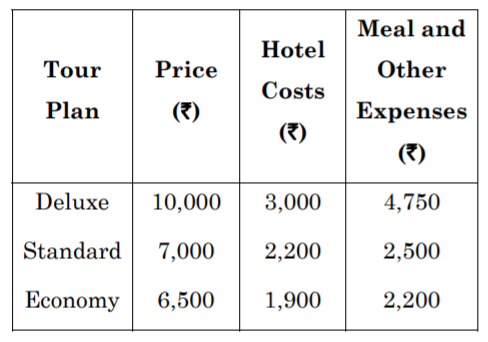
The travel agent wishes to determine the number of packages to offer in each type so as to maximize the total profit. Formulate this as a linear programming problem.
- Find initial basic feasible solution for the following transportation problem using Vogel’s approximation method:
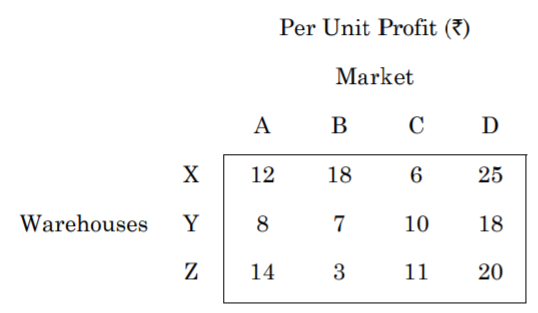
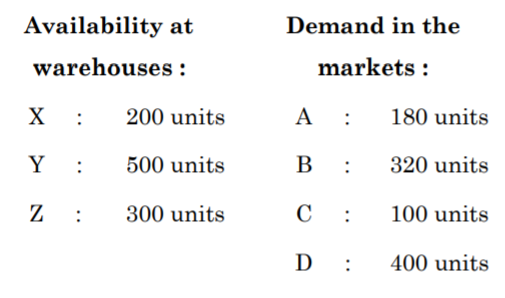
- Write the dual of the following linear programming problem (LPP):
maximise:
z= 10y1 + 8y2 – 6y3
subject to:
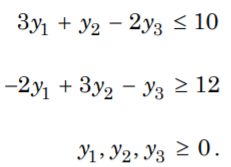
- Using the following data, obtain the economic order quantity (EOQ) and the total variable cost associated with the policy of ordering quantities of that size:
Annual Demand 20,000 Ordering Cost 150 per order inventory carrying cost 24% of average inventory value - Write short notes on any three of the following:
(a) Random experiment and probability
(b) Dynamic programming
(c) Characteristics of a queuing model
(d) Saddle Point
(e) Reasons for using simulation
February, 2021
- (a) What are the main characteristics of Operations Research? Explain with suitable examples. Discuss its scope and limitations.
(b) What is buffer stock? List the reasons for keeping a buffer stock. Suppose the lead time for procurement of a product gets doubled, will you recommend doubling its buffer stock? Justify your answer
- (a) Briefly discuss the application of Quadratic programming in Portfolio selection.
(b) ‘‘Goal programming appears to be the most appropriate, flexible and powerful technique for complex decision problems involving multiple conflicting objectives’’ — Discuss with suitable examples.
- (a) Briefly describe the Cutting Plane Method for solving an Integer Programming Problem.
(b) Explain the concept of Dominance in the context of Game Theory.
- (a) What are the advantages and disadvantages of Monte Carlo simulation as a problem solving technique?
(b) Workers come to the tool store room to receive a special tool (required by them) for accomplishing a particular project assigned to them. The average time between two arrivals is 60 seconds and the arrivals are assumed to be in Poisson distribution. The average service time (of the tool room attended) is 40 seconds.
Dtermine:
(i) Average queue length,
(ii) Average number of workers in the system, including the worker being attended,
(iii) Mean waiting time of an arrival, and
(iv) Average waiting time of an arrival (worker) who waits.
- Write short notes on any four of the following:
(a) Saddle points
(b) ABC Analysis
(c) Periodic review system in inventory system
(d) Travelling Salesman problem
(e) Bellman’s Principle of Optimality
(f) Impact of Web on OR
(a) Solve the following Linear Programming Problem by Graphical method. Min z = 20x1 + 10x2
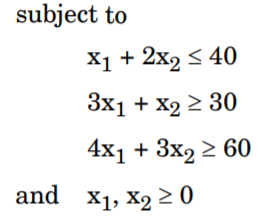
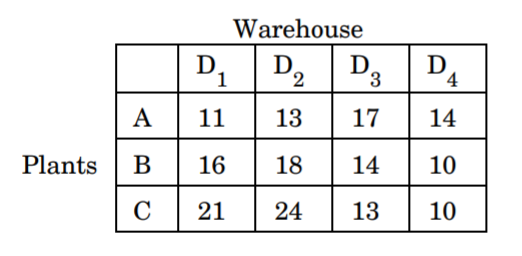
(b) A company has manufacturing plants at places A, B and C with daily production of 250, 300 and 400 units respectively. At points D1 , D2 , D3 and D4 , it has four warehouses with daily demands 200, 225, 275 and 250 respectively. Per unit shipping costs are given in the following table. If the firm wants to minimize its total transportation cost, how should it route its products? Use Vogel’s approximation method to find an initial basic feasible solution.
June, 2020
- (a) “Executive at all levels in business and industry come across the problems of making decisions at every stage in their day-to-day activities. Operations research provides them with various quantitative techniques for decision-making and enhance their ability to make long range plans and solve everyday problems of running a business and industry with greater efficiency, competence and confidence.” Elaborate the statement with suitable examples.
(b) What do you understand by simulation? How is a simulation technique better than mathematical models in solving problems of business and industry? Discuss taking suitable examples.
- (a) What is goal programming? Highlight major differences between linear programming and goal programming
br (b) Explain the Branch and Bound method for solving an integer programming problem. - (a) Discuss the application of dynamic programming in decision-making. How is this different from linear programming?
(b) A motor company purchases 9000 motor spare parts for its annual requirement, ordering one month usage at a time. Each spare part costs 20. The ordering cost Per order is 15 and the carrying charges are 15% of the average inventory per year. You have been asked to suggest more economical purchasing policy for the company. What advice would you offer and how much would it save the company per year?
- (a) What do you understand by ‘Game’ in the context of Game theory? What is the `strategy’ of a player?
(b) A self-service store employs one cashier at its counter. Nine customers arrive on an average every 5 minutes while the cashier can serve 10 customers in 5 minutes. Assuming Poisson distribution for arrival rate and exponential distribution for service time, find:
- Average number of customers in the system,
- Average number of customers in the queue,
- Average time a customer spends in the system, and
- Average time a customer waits before being served.
- (a) Solve the following Linear Programming Problem by Graphical method: Min z = 4x1 — 2x2
subject to:

(b) A company has three plants at A, B and C which supply warehouses located at D1 ,D2,D3and D4. Daily plant capacities are 11, 13 and 19 respectively. Daily warehouse requirements are 6, 6, 8 and 23 respectively. The unit transportation costs in Rupees are given below:
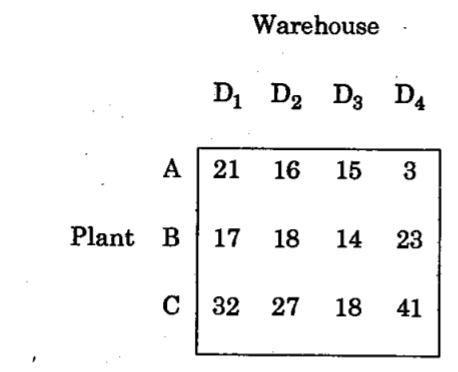
Determine an optimum distribution for the company in order to minimize the total transportation cost by Vogel’s approximation method. How much is the cost?
- 6. Write short notes on any four of the following:
(a) Buffer stock
(b) Degeneracy in LP problem
(c) North West Corner rule
(d) Sensitivity Analysis
(e) 2 x n games
(0 Unbounded solution
Also view
- IGNOU Course details and sample paper link
- Sample paper of ignou for exam
- Solved Assignments of IGNOU courses
Total Views: 40
